bresenham

ブレゼンハムの直線アルゴリズム

　プログラムの専門的なことになるので興味が無い人は読み飛ばしてもらいたい。

　処理に時間のかかる乗算や除算を使用せず、加算と減算のみで任意の2点間に直線を描画するプログラムに、
　”bresenham”というアルゴリズムがある。
　これは主にペイントソフトなどの直線描画に使われている。
　だがこのプログラムは加減算しか使用しない代わりに分岐処理が非常に多く、
　過去のCPUならいざ知らず最近のものは分岐予測機能を持ちシフト演算も早いため、必ずしも効率的なアルゴリズムではない。

　具体的には、まず始点と終点の間の距離をXY方向ともに計測し、結果符号を座標更新時の方向用に記憶しておき計測値の絶対値をとる。
　そして、計測値の大きいほうをベース値、もう一方を更新値とし、カウンタをゼロクリアする。
　ここまでが初期化で、次からが実際の繰り返し処理となる。
　カウンタに更新値を加算、カウンタがベース値を超えていたらベース値にしたほうの座標を更新し、
　カウンタからベース値を引いて、さらに加算値の方向の座標も更新する。
　これを座標が目的地にたどり着くまで繰り返す。

　Javaソースでは以下のようになる

    // ⊿xと⊿yを2倍してdeltaX、deltaYとする
   deltaX = Math.abs(deltaX * 2)；
   deltaY = Math.abs(deltaY * 2)； 
        
   if (deltaX > deltaY)
　 {
        fraction = deltaY - deltaX / 2；  // fractionの初期値
        while (nextX != end.x)
　 　　{
            // fraction>=0のときはQ(a+i+1,b+j+1)を選ぶ
           // つまり、nextX,nextYともに+1
            if (fraction >= 0)
　　　　　 {
                nextY += stepY；      // yが1増えると
                fraction -= deltaX；  // fractionはdeltaX減る
            }
            // fraction<0のときはP(a+i+1,b+j)を選ぶ
            // つまり、nextXだけ+1
            nextX += stepX；      // xが1増えると
            fraction += deltaY；  // fractionはdeltaY増える
            line[step] = new Point(nextX, nextY)；
            step++；
        }
    }

具体的な説明

　始点を(a,b)、終点を(a+⊿x,b+⊿y)、⊿x＞⊿y＞0とし、この間に直線を引くことを考える。
　ある場所◎(a+ i,b+j)において次に塗りつぶすマスは⊿x＞⊿yという条件ではP(a+i+1,b+j)かQ(a+i+1,b+j+1)のどちらか。
　下図の◎の次に塗りつぶすマスとしてPとQのどちらがよいかを判定するのがプログラム中の変数fraction。

　

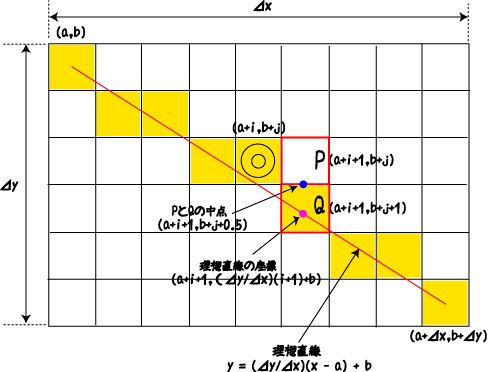
　(a,b)と(a+⊿x,b+⊿y)をつなぐ理想的な直線の方程式は、
　　　y = (⊿y/⊿x)(x - a) + b

　x=a+i+1における理想的なy座標は上の方程式にx=a+i+1を代入して
　　　y = (⊿y/⊿x)(a+i+1-a) + b
　　　　= (⊿y/⊿x)(i+1) + b

　PとQの中点のy座標は( (b+j)+(b+j+1) )/2より
　　　b+j+0.5

　ここで、x=a+i+1における理想曲線のy座標とPとQの中点のy座標の差は
　　fraction' = (⊿y/⊿x)(i+1) + b - (b+j+0.5)

　fraction'が正ならば理想曲線のy座標はPよりはQにより近い。
　fraction'が負ってことは理想曲線のy座標はQよりはPに近い。
　従って
　fraction' ≧ 0 ならば Q を選ぶ
　fraction' ＜ 0 ならば P を選ぶ

　fraction'は式の中に0.5という小数があるため、fraction'を2⊿x倍してfractionとすると
　　fraction = 2⊿x * fraction'
　　　　　　　= 2⊿y(i + 1) - ⊿x(2j + 1)

　i（x方向）を1増やすとfractionは2⊿y増える
　j（y方向）を1増やすとfractionは2⊿x減る

　fonction初期値を(i,j)=(0,0)とすると、
　　2⊿y-⊿x

　ここで2⊿xをdeltaX、2⊿yをdeltaYに置き換えると、
　　i（x方向）を1増やすとfractionはdeltaY増える
　　j（y方向）を1増やすとfractionはdeltaX減る
　　fractionの初期値はdeltaY-deltaX/2

　ここまでがROでの計算値で、直線微妙な歪みが出る。

　歪みを一切なくすには
　fonction初期値を(4,8)にしてやればよい。

　上に戻る

　上に戻る

　考察TOPに戻る